[mathjax]
 (2)
\(t=\log_2 x~\)とおくと,\(~8~\verb|<|~x~\verb|<|~32~\)より\(~3~\verb|<|~t~\verb|<|~5~\)
\[
\begin{align*}
f(x)=&-t^3+3t^2+24t-72 \\
=&g(t)-72
\end{align*}
\]
よって\(~f(x)~\)が最大となるのは\(~t=4~\)すなわち\(~x=16~\)のときであり,\(~\)その最大値は
\[
g(4)-72=8 \quad \cdots (答)
\]
(2)
\(t=\log_2 x~\)とおくと,\(~8~\verb|<|~x~\verb|<|~32~\)より\(~3~\verb|<|~t~\verb|<|~5~\)
\[
\begin{align*}
f(x)=&-t^3+3t^2+24t-72 \\
=&g(t)-72
\end{align*}
\]
よって\(~f(x)~\)が最大となるのは\(~t=4~\)すなわち\(~x=16~\)のときであり,\(~\)その最大値は
\[
g(4)-72=8 \quad \cdots (答)
\]
過去問を利用して、久留米大学医学部推薦入試の数学について学びましょう。 平成28年度は全部で5問出題されました。 そのうちの4番について、問題と解答を以下にまとめています。 さらに詳しい解説授業は、別の記事にしています。
平成28年度(2016)推薦入試[4]
問題
次の(1),(2)の問いに答えよ。
- \(-x^3+3x^2+24x-m=0~\)が2つの異なる正の解と1つの負の解を持つような定数\(~m~\)の値の範囲を求めよ。
- 関数\(~f(x)=-\left( \log_2x \right)^3+3\left(\log_2x \right)^2+8\log_2x^3 -72~\)の\(~8~\verb|<|~x~\verb|<|~32~\)における最大値と,その最大値をとるときの\(~x~\)の値を求めよ。
久留米推薦(平成28年度)
解答
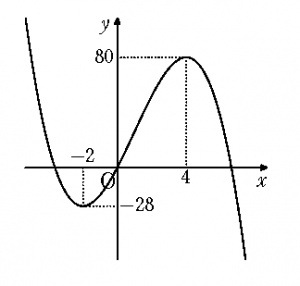
(1) 与えられた3次方程式より \[ \begin{align*} -x^3+3x^2+24x=m \end{align*} \] \(g(x)=-x^3+3x^2+24x~\)とおくと,\(~g'(x)=-3(x+2)(x-4),~g(-2)=-28,~g(4)=80~\)より,\(~\)増減表は以下の通り。 \[ \begin{array}{|c|*5{c|}}\hline x & \cdots & -2 & \cdots & 4 & \cdots \\ \hline g'(x) & – & 0 & + & 0 & – \\ \hline g(x) & \searrow & -28 & \nearrow & 80 & \searrow \\ \hline \end{array} \] 与えられた3次方程式の実数解は,\(~y=g(x)~\)と\(~y=m~\)のグラフの共有点の\(~x~\)座標に一致する。したがってグラフより,\(~\)3次方程式が2つの異なる正の解と1つの負の解をもつような定数\(~m~\)の値の範囲は \[ 0~\verb|<|~m~\verb|<|~80 \quad \cdots (答) \] (2)
\(t=\log_2 x~\)とおくと,\(~8~\verb|<|~x~\verb|<|~32~\)より\(~3~\verb|<|~t~\verb|<|~5~\)
\[
\begin{align*}
f(x)=&-t^3+3t^2+24t-72 \\
=&g(t)-72
\end{align*}
\]
よって\(~f(x)~\)が最大となるのは\(~t=4~\)すなわち\(~x=16~\)のときであり,\(~\)その最大値は
\[
g(4)-72=8 \quad \cdots (答)
\]
(2)
\(t=\log_2 x~\)とおくと,\(~8~\verb|<|~x~\verb|<|~32~\)より\(~3~\verb|<|~t~\verb|<|~5~\)
\[
\begin{align*}
f(x)=&-t^3+3t^2+24t-72 \\
=&g(t)-72
\end{align*}
\]
よって\(~f(x)~\)が最大となるのは\(~t=4~\)すなわち\(~x=16~\)のときであり,\(~\)その最大値は
\[
g(4)-72=8 \quad \cdots (答)
\]
さらに詳しい解説授業もあります
この問題でさらに力をつけよう!詳しい解説授業はこちら






