[mathjax]
過去問を利用して、久留米大学医学部推薦入試の数学について学びましょう。 平成30年度は全部で5問出題されました。 そのうちの5番について、問題と解答を以下にまとめています。 さらに詳しい解説授業は、別の記事にしています。
平成30年度(2018)推薦入試[5]
問題
- 辺の長さが\(a=2\)のとき,頂点\(\rm{C}\)の座標を求めなさい。
- 正方形の面積が最大となるときの辺の長さ\(a\)を求めなさい。
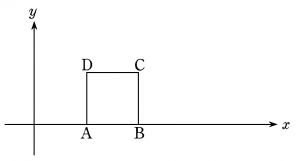
久留米推薦(平成30年度)
解答
正方形の1辺の長さは\(a\)なので,点\(\rm{A}\)の座標を\(\rm{A}\)\((p,~0)\)とすると,他の3点は\(\rm{B}\)\((p+a,~0),~\rm{C}\)\((p+a,~a),~\rm{D}\)\((p,~a)\)となる。
また,各頂点の\(x\)座標が\(0 \lt x \lt 7\)の範囲にあるので
\begin{align*} 0 \lt a \lt 7~~\text{かつ}~~0 \lt p+a \lt 7 \quad \cdots [1] \end{align*} 点\(\rm{D}\)は曲線\(y=-\displaystyle \frac{1}{60}x(x-7)(x+7) \)上にあるので \[ a=-\displaystyle \frac{1}{60}p(p-7)(p+7) \quad \cdots [2] \]
(1)\(\quad ~a=2\)とする。\([2]\)より
\begin{align*} -\displaystyle \frac{1}{60}p(p-7)(p+7)&=2 \\ -p(p^2-49)&=120 \\ p^3-49p+120&=0 \\ (p-3)(p-5)(p+8)&=0 \end{align*}
\(\quad \)\([1]\)を満たすのは\(p=3\)のみである。\\ したがって,\(\rm{C}\)\((5,~2) \cdots \text{(答)}\)
(2)\(\quad ~~\)正方形の面積が最大となるのは,正方形の1辺の長さ\(a\)が最大となるときである。[1],[2]をともに満たす\(a\)の最大値を求める。
\(f(x)=-\displaystyle \frac{1}{60}x(x-7)(x+7) \)とおくと
\begin{align*} f'(x)&=-\displaystyle \frac{1}{60} \left\{ (x-7)(x+7)+x(x+7)+x(x-7) \right\} \\ &=-\displaystyle \frac{1}{60}(3x^2-49) \end{align*}
\(\quad 0 \lt x \lt 7\)の範囲で\(f'(x)=0\)として\(x=\displaystyle \frac{7}{\sqrt3}.\)
増減表は
\begin{array}{c|ccccc} x & 0 & \cdots & \displaystyle \frac{7}{\sqrt3} & \cdots & 7 \\ \hline f’(x) & & + & 0 & – & \\ \hline f(x) & & \nearrow & f\left( \frac{7}{\sqrt3} \right) & \searrow & \end{array}
\(\quad\)また,\(~[1]\)より点\(\rm{D}\)が存在する領域は\( 0 \lt x \lt 7,~-x \lt y \lt -x+7 \)を満たす領域であるから,点\(\rm{D}\)の軌跡は下図のとおり。
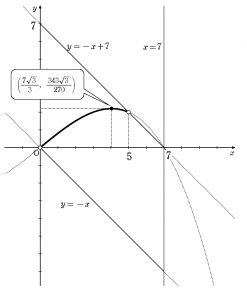
したがって,正方形の面積が最大となるときの辺の長さは
\begin{align*} a&=f\left( \frac{7}{\sqrt3} \right) \\ &=-\displaystyle \frac{1}{60} \cdot \displaystyle \frac{7}{\sqrt3} \left( \displaystyle \frac{7}{\sqrt3}-7 \right) \left( \displaystyle \frac{7}{\sqrt3}+7 \right) \\ &=-\displaystyle \frac{7^3}{60} \cdot \displaystyle \frac{\sqrt3}{3} \left( \displaystyle \frac{1}{\sqrt3}-1 \right) \left( \displaystyle \frac{1}{\sqrt3}+1 \right) \\ &=-\displaystyle \frac{7^3}{60} \cdot \displaystyle \frac{\sqrt3}{3} \left( \displaystyle \frac{1}{3}-1 \right) \\ &=\displaystyle \frac{343 \sqrt3}{270} \cdots \text{(答)} \end{align*}
さらに詳しい解説授業もあります
この問題でさらに力をつけよう!詳しい解説授業はこちら






