過去問を利用して、久留米大学医学部推薦入試の数学について学びましょう。 令和3年度入試では全部で5問出題されました。 そのうちの3番について、問題と解答を以下にまとめています。 さらに詳しい解説授業は、別の記事にしています。
令和3年度(2021)推薦入試[3]
問題
関数\(~y=8^{\frac{x}{2}}+8^{-\frac{x}{2}}-3\cdot2^x-3\cdot2^{-x}-6\cdot2^{\frac{x}{2}}-6\cdot2^{-\frac{x}{2}}+4~\)について,次の問いに答えよ。
- \(t=2^{\frac{x}{2}}+2^{-\frac{x}{2}}\)とおくとき,\(y~\)を\(~t~\)の式で表すと\(\boxed{\Large\phantom{ppp}}\)である。
- \(x~\)がすべての実数をとって変化するとき,\(t~\)のとりうる値の範囲は\(\boxed{\Large\phantom{ppp}}\)である。
- \(x~\)がすべての実数をとって変化するとき,\(y~\)の最小値は\(\boxed{\Large\phantom{ppp}}\)であり,そのときの\(~x~\)の値は\(~x=\log_2\left( \boxed{\Large\phantom{ppp}} \right) -1~\)である。
久留米推薦(令和3年度入試)
解答
- \(t=2^{\frac{x}{2}}+2^{-\frac{x}{2}}\)より \begin{align*} t^2=& \left(2^{\frac{x}{2}} \right)^2+ 2\cdot2^{\frac{x}{2}} \cdot 2^{-\frac{x}{2}} +\left(2^{-\frac{x}{2}} \right)^2 \\ =& 2^x+2+2^{-x} \\ \therefore 2^x+2^{-x}=& t^2-2 \\ t^3=& \left(2^{\frac{x}{2}} \right)^3+ 3\cdot \left(2^{\frac{x}{2}}\right)^2 \cdot 2^{-\frac{x}{2}} +3\cdot 2^{\frac{x}{2}} \cdot \left( 2^{-\frac{x}{2}} \right)^2 +\left(2^{-\frac{x}{2}} \right)^3 \\ =& 8^{\frac{x}{2}}+3\cdot 2^{\frac{x}{2}}+3\cdot 2^{-\frac{x}{2}}+8^{-\frac{x}{2}} \\ \therefore 8^{\frac{x}{2}}+8^{-\frac{x}{2}}=& t^3-3t \end{align*} したがって \begin{align*} y=&(8^{\frac{x}{2}}+8^{-\frac{x}{2}})-3(2^x+2^{-x}) -6(2^{\frac{x}{2}}+2^{-\frac{x}{2}})+4 \\ =&(t^3-3t)-3(t^2-2)-6t+4 \\ =&t^3-3t^2-9t+10 \cdots \textrm{(答)} \end{align*}
- \(2^{\frac{x}{2}}>0,~2^{-\frac{x}{2}}>0~\)であるから,相加平均と相乗平均の関係により \begin{align*} 2^{\frac{x}{2}}+2^{-\frac{x}{2}} \geqq & 2 \sqrt{2^{\frac{x}{2}} \cdot 2^{-\frac{x}{2}}} \\ t \geqq & 2 \cdots \textrm{(答)} \end{align*} 等号は\(~2^{\frac{x}{2}}=2^{-\frac{x}{2}}~\)すなわち\(~x=0~\)のとき成り立つ。
- \(f(t)=t^3-3t^2-9t+10~\)とおくと
\begin{align*}
f'(t)=& 3t^2-6t-9 \\
=& 3(t+1)(t-3)
\end{align*}
\(t \geqq 2~\)において\( ~f'(t)=0~\)を満たすのは\(~t=3~\)である。
\(t \geqq 2~\)における増減表は
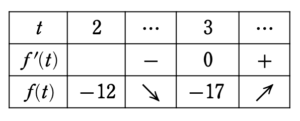 よって\(~y~\)は,\(t=3~\)で最小値\(~-17 \cdots \textrm{(答)}\)をとる。
よって\(~y~\)は,\(t=3~\)で最小値\(~-17 \cdots \textrm{(答)}\)をとる。
\(t=3~\)のとき
\begin{align*} 2^{\frac{x}{2}}+2^{-\frac{x}{2}}=&3 \\ \left(2^{\frac{x}{2}}\right)^2-3\cdot 2^{\frac{x}{2}}+1=&0 \\ 2^{\frac{x}{2}}=&\frac{3 \pm \sqrt{5}}{2} \\ \frac{x}{2}=&\log_2 \frac{3 \pm \sqrt{5}}{2} \\ x=&\log_2 \left(\frac{3 \pm \sqrt{5}}{2}\right)^2 \\ =&\log_2 (7 \pm 3\sqrt{5}) -1 \cdots \textrm{(答)} \end{align*}
さらに詳しい解説授業もあります
この問題でさらに力をつけよう!詳しい解説授業はこちら
※誤植やミスを見つけた方は,ぜひお知らせください。





