平成29年度(2017)久留米大学医学部推薦入試数学過去問の解説授業（３／５）

[mathjax]

この記事には，久留米大学医学部の過去問の詳しい解説が載っています。過去問を通して久留米大学医学部の数学について学べるように，授業のような解説にしています。これまで勉強してきたことを整理し、あなたの数学力をレベルアップしましょう！

解答はすでにこちらの記事で示しております。

平成29年度(2017)久留米大学医学部推薦入試数学［３］

平成29年度(2017)久留米大学医学部推薦入試数学［３］

方程式と数列の複合問題

方程式が整数解を持つ、という条件から数列を作るという、2つの分野にまたがった複合問題です。そのため、ややとまどった受験生も多かったようです。

あなたはどちらで解く？方程式の2つの解法

今回は、2つの解法を示しました。その理由は、方程式の問題へのアプローチについて考えてほしかったからです。方程式は、大きく分けると2つの解法が存在します。初めて聞きましたか？解説しましょう。方程式は、解を求めることができます。2次方程式ならば解の公式を使えば、形はどうあれ、とりあえず解を求めることはできます。その素直な思考の流れから、解を求めてそれが整数解となるように条件を考えたのが、【解答その１】です。思考が素直なので、誰もがわかりやすい解答だと思います。でも、それ以外に方程式の問題を解くアプローチとして、何か無かったでしょうか。それは、【解答その２】のようにグラフを利用する解法です。受験勉強をそれなりにしてきた人ならば、方程式の問題はたくさん解いているはずです。でもその解き方について、【解答その１】のように素直に方程式の解を調べていく解法と、【解答その２】のようにグラフを用いて解く解法があることを意識している人はどれだけいるでしょう。方程式の問題を目の前にしたときに、自分はどちらの解法を用いて解こうとしているのか、ぜひ意識してください。そうすることで、解法についての理解が深まり、複数の解法で解くことができる柔軟な力を身につけることができるでしょう。

解の公式で解を求めてから考える【解答その１】

解を求めることについては、解の公式を使うだけだから何も難しいことはないと思います。方程式より

\[ \begin{align*} x^2-2x-a+\frac{1}{2}=&0 \\ x=&1 \pm \sqrt{1-\left( -a+ \frac{1}{2} \right)} \\ =&1 \pm \sqrt{a+ \frac{1}{2}} \end{align*} \]

それよりも、計算して出てきた解が偶数解である、というのをどのように解釈するかがポイントです。

与えられた方程式が整数解をもつ条件は\( ~\sqrt{a+ \frac{1}{2}}~ \)が奇数であることである。

ルートの外に、1があるので、ルートの部分は奇数となるはずです。それがわかれば、以下のように式を立てて解くだけです。

その奇数を自然数\(k\)を用いて\(~2k-1~\)とし,そのときの\(a\)の値を\(a_k\)とすると \[ \begin{align*} \sqrt{a_k+ \frac{1}{2}}=2k-1 \\ a_k+ \frac{1}{2}=\left(2k-1\right)^2 \\ a_k=4k^2-4k+\frac{1}{2} \end{align*} \] \(~k~\)は自然数であるから，\(~a_k~\)は単調に増加する。

答えは\(~n~\)で書かなければならないので、\(k~\)を\(~n~\)に置き換えて解答しましょう。\(a_n\)が単調に増加していることに言及すれば完璧です。 (3)は計算するだけですので省略します。

グラフを用いて方程式の解を視覚化する【解答その２】

方程式の左辺を\(~f(x)~\)とおくことで、方程式の実数解は、放物線\(~y=f(x)~\)と直線\(~y=0\)（つまりx軸）との共有点として可視化できます。

\(~f(x)=2x^2-4x-2a+1~\)とおくと，\(~y=f(x)~\)の軸は\(~x=1~\)である。

方程式が偶数解をもつということは、放物線と\(~x~\)軸の共有点の\(~x~\)座標が偶数となるように、放物線の位置を決めればいいことが分かります。軸が\(~x=1~\)であることから、偶数解は\(~0と2,ｰ2と4,-4と6,\cdots \)となります。\(k\)番目の解の組み合わせは、\(2k\)と\(2-2k\)であることがわかります。放物線の対称性を考えると分かりやすいでしょう。

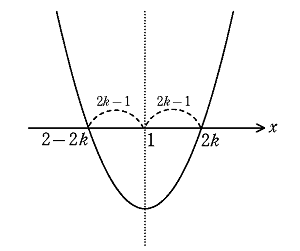
\(~k~\)を自然数として，方程式\(~2x^2-4x-2a+1=0~\)が偶数解\(~x=2k~\)をもつとき，下図よりもう一方の解は\(~x=2-2k~\)である。

ここまでわかれば、\(f(x)~\)は\(~(x-2k)~\)と\(~\{ x-(2-2k) \} \)で因数分解できて、恒等式\(~2（x-2k)(x-2+2k)~\)を作ることができます。\(x^2~\)の係数が\( 2 \)になっていることに注意しましょう。あとは恒等式であることから、定数項を比較して\( a_k \)を決定できます。

このときの定数\(~a~\)を\(~a_k~\)とすると，次の恒等式が成り立つ。 \[ \begin{align*} 2x^2-4x-2a_k+1=2(x-2k)(x-2+2k) \end{align*} \] 両辺の定数項を比較して \[ \begin{align*} -2a_k+1=&4k(2-2k) \\ a_k=&4k^2-4k+\frac{1}{2} \end{align*} \] \(~k~\)は自然数であるから，\(~a_k~\)は単調に増加する。

この問題のポイント

振り返ってみましょう。

この問題のポイントは、何と言ってもこれです。

方程式の問題を、「解そのものを調べる」解法と、「グラフを用いて共有点を調べる」解法の、どちらでも解くことが出来る。

問題を解くときに、自分がどういう方針で解こうとしているのか、常に意識しましょう。

解法その１と解法その２、それぞれのポイントについては、以下の通りです。

（解法その１）解が偶数であることを、条件式にすることが出来る。
（解法その２）2次関数の対称性に気付き、2つの整数解を\( k~\)を用いて表すことができる。
（解法その２）恒等式を作り、定数項を比較することに気付くことが出来る