[mathjax]
過去問を利用して、久留米大学医学部推薦入試の数学について学びましょう。 平成29年度は全部で5問出題されました。 そのうちの1番について、問題と解答を以下にまとめています。 さらに詳しい解説授業は、別の記事にしています。
平成29年度(2017)推薦入試[1]
問題
[1] 実数\(~x, \ y~\)について,\(~x^2+xy+y^2-3x-3y=0~\)が成り立つとき,\(~xy~\)のとりうる値の範囲を求めよ。
久留米推薦(平成29年度)
解答
\(x+y=u, \ xy=v \)とおくと,方程式より \begin{align} x^2+xy+y^2-3x-3y=&0 \\ (x+y)^2-xy-3(x+y)=&0 \\ u^2-v-3u=&0 \\ v=\left( u-\frac{3}{2} \right)^2 &-\frac{9}{4}\qquad \cdots [1] \end{align} 実数\(~x, \ y~\)は,2次方程式\(~t^2-ut+v=0~\)の実数解であるから,判別式を\(D\)として \begin{align} D=&u^2-4v \geqq 0 \\ ∴ v &\leqq \frac{1}{4}u^2 \qquad \qquad \qquad \qquad \cdots [2] \end{align} [1]と\(~v=\frac{1}{4} u^2~\)の交点の座標は\(~(0, 0), (4, 4)~\)であるから,[1], [2]をともに満たす領域は下図の通り。
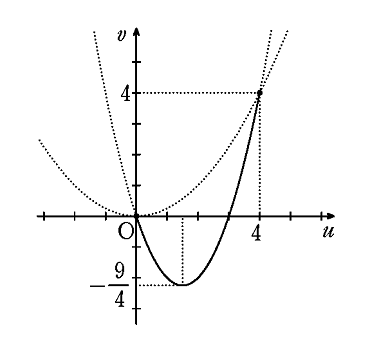
したがって,\(~xy=v~\)のとりうる値の範囲は \begin{eqnarray*} -\frac{9}{4} \leqq xy \leqq 4 \qquad \qquad \qquad \cdots (答) \end{eqnarray*}
さらに詳しい解説授業もあります
この問題でさらに力をつけよう!詳しい解説授業はこちら







