[mathjax]
この記事には,久留米大学医学部の過去問の詳しい解説が載っています。過去問を通して久留米大学医学部の数学について学べるように,授業のような解説にしています。これまで勉強してきたことを整理し、あなたの数学力をレベルアップしましょう!
解答はすでにこちらの記事で示しております。
平成28年度(2016)久留米大学医学部推薦入試数学[4]
一見,別の問題のように見えますが・・・
大問4は微分の問題です。小問が2問,問われているのはそれぞれ次の通りです。
- 方程式の実数解について,グラフを用いて調べることができるか
- 適切な置き換えをして,対数関数の最大値を求めることができるか
(1)は,いわゆる「定数分離法」を用いる定番の手法です。 (2)も\(~\log_2x=t~\)と置くだけで3次関数に帰着できるので,解法について迷うことは無いと思います。
なお,(1)と(2)は全く独立した問題のように見えますが,3次関数の形がほとんど同じです。 そのことに気付けば,解答時間を短縮することができます。 出題者の意図を読み取りましょう。
方程式の実数解を視覚化せよ
まず(1)について解説します。
方程式の実数解について調べたいときに,グラフを用いることは有効な手法です。 右辺と左辺をそれぞれ\(~y~\)と置くことで,方程式を\(~y=\)(左辺)と\(~y=\)(右辺)の連立方程式と見なすのです。
すると,方程式の実数解は,2つのグラフの共有点の\(~x~\)座標と一致することになります。 こうして方程式の実数解を視覚化することができます。
方程式は移項することで右辺と左辺の組合せを変えることができるので,解きやすい形を自分で考えることになります。今回の問題は,文字定数\(~m~\)を右辺に移項して,3次関数のグラフと定数関数\(~y=m~\)(\(x~\)軸に平行な直線)のグラフを使って調べます。
これがいわゆる「定数分離法」のオーソドックスな形です。
\(m~\)の値を変化させると直線が上下に動きますが,3次関数は決定している(動かない)ので,とてもわかりやすくなります。
この問題,定数\(~m~\)を分離しないで解くことはできないのでしょうか。
結論から言うと,できますがややわかりにくくなります。
定数\(~m~\)をそのままにした場合,左辺は定数\(~m~\)を含んだ3次関数,右辺は\(~y=0~\)(つまり\(x~\)軸)となります。 \(~m~\)の値を変化させると動くのが3次関数なので,ややわかりにくくなるのです。
グラフ化したのに解けない人は,何が足りないのか
「ああ定数分離法ね。知ってるよ」という人は多いと思います。
しかし,「定数分離法」を知っているのにこの問題を解けない人は,意外と多いのではないかと思います。
解法を知っているのに解けないのはなぜでしょうか。
それは,『知っている』けれども『理解が浅い』からです。
今回の問題のベースになっているのは,よくある定数分離法の問題「3次方程式が異なる3つの実数解をもつ定数\(~m~\)の値の範囲を求めよ」というものです。 どんな教科書にも載っている問題なので,受験生であれば誰でも目にしたことがある問題です。 実数解が3つならば共有点を3つ持つように直線を動かせばよいので,答えが(極小値)\(\verb|<|~m~\verb|<|\)(極大値)となることはわかるでしょう。
でも今回の推薦入試の問題は「異なる2つの正の解と1つの負の解をもつように定数\(~m~\)の値の範囲を求めよ」です。
正負について問われているので,少し難しくなっています。どこを見ればいいのでしょうか。
答えはこれまでの文章の中にあります。気付くことはできますか?
少し前に,以下のように記述していますね。
「方程式の実数解は,2つのグラフの共有点の\(~x~\)座標と一致することになります。」
そうです。
「実数解と共有点」が一致するのではなく,「実数解と共有点の\(~x~\)座標」が一致するのです。
ここまでしっかりと理解していれば,共有点の\(~x~\)座標の正負を見ればよいことがわかります。
これまで軽く考えて浅い理解で解いていた人は,ここでしっかりと記憶に刻みましょう。
与えられた3次方程式の実数解は,\(~y=g(x)~\)と\(~y=m~\)のグラフの共有点の\(~x~\)座標に一致する。
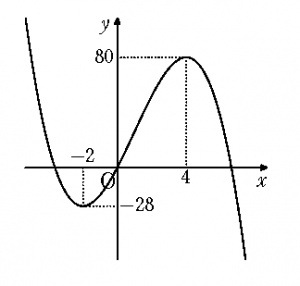
したがってグラフより,3次方程式が2つの異なる正の解と1つの負の解をもつような定数\(~m~\)の値の範囲は
\[ 0~\verb|<|~m~\verb|<|~80 \quad \cdots (答) \]もしあなたが浅い理解しかしていない人であっても,教科書レベルの問題なら解くことができます。正解するのですから,自分の欠点には気付かないでしょう。
やや難しめの問題を解くことでやっと,自分の理解が浅かったことに気付くことができるのです。 基礎となる問題と入試問題とのつながりを意識して,理解が深まるような勉強をしていきましょう。
置き換えは簡単だけれども・・・
次に(2)について解説します。 \(\log_2x=t~\)の置き換えについてはすぐに気付くでしょう。 置き換えのときに注意することは何でしょうか。 そう,置き換えた変数\(~t~\)の範囲について調べることです。
今回は\(~8~\verb|<|~x~\verb|<|~32~\)ですから対数をとって\(~\log_2{8}~\verb|<|~\log_2{x}~\verb|<|~\log_2{32}~\)すなわち\(~3~\verb|<|~t~\verb|<|~5~\)です。
あとはこの範囲で,置き換えた\(~t~\)の3次関数の最大値を求めればよいのですが,3次関数の形が(1)の3次関数とほぼ同じ形となっています。
違うところは定数項のみなので,(1)の3次関数を\(~y~\)軸方向に平行移動したグラフであることがわかります。
ということは最大値をとる\(~x~\)の値は変わらないことになりますから,解答のようにすぐに最大値を求めることができるというわけです。
もう一度微分して増減表を書いてしまった人は,視野が狭くなるタイプかもしれませんね。一歩引いたところから問題全体を見るようにしましょう。
似ているものを探すこと,共通点を見いだすことはとても大切なことです(例えば,相似な図形を見つけることができればあっさり解ける問題などがありますね)。 答えを知って満足するのではなく,解いた問題から教訓を得て,次の問題を解くときにその経験を活かしましょう。
この問題のポイント
振り返ってみましょう。
この問題が解けるかどうかのポイントは,
- 定数分離法に気付くことができる
- 方程式の実数解について,グラフを用いて調べることができる
- 一致するのは,「方程式の実数解」と「共有点の\(~x~\)座標」であることを正しく理解している
- 適切な置き換えをして,対数関数の最大値を求めることができる
- (1)と(2)の3次関数が似ていることに気付き,それを利用することができる
といったところです。自分に足りないモノがあれば,しっかりと身に付けておきましょう。






