[mathjax]
この記事には，久留米大学医学部の過去問の詳しい解説が載っています。過去問を通して久留米大学医学部の数学について学べるように，授業のような解説にしています。これまで勉強してきたことを整理し、あなたの数学力をレベルアップしましょう！
解答はすでにこちらの記事で示しております。
平成28年度(2016)久留米大学医学部推薦入試数学［３］
最近増えているベクトルの問題
大問３は平面ベクトルの問題です。 以前は「久留米大学医学部ではベクトルは出題されない」と言っていたものですが，最近は推薦試験・一般試験とも出題されるようになりました。 しかしそのほとんどは空間ではなく平面ベクトルの問題です。 ですからまず，平面ベクトルを中心に対策しておきましょう。
まずは問題文を正確に読み取り,図を書こう
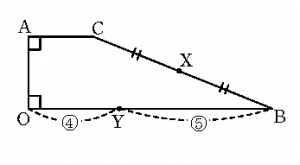(1) 上図より \[ \begin{align} \overrightarrow{\mathrm{OX}}=&\dfrac12\overrightarrow{\mathrm{OB}}+\dfrac12 \overrightarrow{\mathrm{OC}} \\ =&\dfrac12 \overrightarrow{\mathrm{OB}}+\dfrac12 \left( \overrightarrow{\mathrm{OA}} + \overrightarrow{\mathrm{AC}} \right) \\ =&\dfrac12 \vec{b}+ \dfrac12 \left( \vec{a}+ \dfrac13 \vec{b} \right) \\ =& \dfrac12 \vec{a}+ \dfrac23 \vec{b} \end{align} \] したがって \[ \begin{align*} \overrightarrow{\rm{AX}}=&\overrightarrow{\rm{OX}}-\overrightarrow{\rm{OA}} \\ =&\left( \dfrac{1}{2}\vec{a}+\dfrac{2}{3}\vec{b} \right)-\vec{a} \\ =&-\dfrac{1}{2}\vec{a}+\dfrac{2}{3}\vec{b} \quad \cdots \text{（答）} \end{align*} \] (2) \[ \begin{align*} \overrightarrow{\rm{YX}}=&\overrightarrow{\rm{OX}}-\overrightarrow{\rm{OY}} \\ =&\left( \dfrac{1}{2}\vec{a}+\dfrac{2}{3}\vec{b} \right)-\dfrac{4}{9}\vec{b} \\ =&\dfrac{1}{2}\vec{a}+\dfrac{2}{9}\vec{b} \quad \cdots \text{（答）} \end{align*} \]前半部分は，図をきちんと書いて，ベクトルの和・差を使えば答は出せると思います。 解答例とは違うやり方であっても何ら問題はありません。 (1)(2)は絶対に解きましょう。
直角という条件から内積の式を立てる
後半は，直角という条件から「内積イコール0」の式を立てます。 あとは計算手順に従っていけば答は自動的に導かれます。
(3) \( \angle {\rm{AYX}}=\dfrac{\pi}{2}~\)のとき,\(~\rm{AY} \perp \rm{YX}\)すなわち\(~\overrightarrow{\rm{AY}} \cdot \overrightarrow{\rm{YX}}=0~\)である。\(~\overrightarrow{\rm{AY}}=\overrightarrow{\rm{OY}}-\overrightarrow{\rm{OA}}=-\vec{a}+\dfrac{4}{9}\vec{b}~\)であるから \[ \begin{align*} \left( -\vec{a}+\dfrac{4}{9}\vec{b} \right)\cdot \left( \dfrac{1}{2}\vec{a}+\dfrac{2}{9}\vec{b} \right)=&0 \\ -\dfrac12 \left( \vec{a}-\dfrac{4}{9}\vec{b} \right)\cdot \left( \vec{a}+\dfrac{4}{9}\vec{b} \right)=&0 \\ |\vec{a}|^2-\dfrac{16}{81}|\vec{b}|^2=&0 \end{align*} \] \( |\vec{b}|=3r\)なので \[ \begin{align*} |\vec{a}|^2-\dfrac{16}{81}(3r)^2=&0 \\ |\vec{a}|^2=&\dfrac{16}{9}r^2 \end{align*} \] したがって \[ \mathrm{OA}=|\vec{a}|=\dfrac{4}{3}r \quad \cdots \text{（答）} \]
ベクトルの問題はこのように，問題文の設定にしたがって式を立てれば，あとは手順通り解いていけば答えが出るものです。 この流れをつかめば，ベクトルが得意になれるはずです。 早くマスターしておきましょう。
この問題のポイント
振り返ってみましょう。
この問題が解けるかどうかのポイントは、
- ベクトルの和と差・実数倍を用いることができる
- 直角から内積=0に気付くことができる
- 立てた式を手順通りに解くことができる
特に難しいところはありません。完答しましょう。
