[mathjax]
この記事には,久留米大学医学部一般入試過去問の詳しい解説が載っています。過去問を通して久留米大学医学部の数学について学べるように,授業のような解説にしています。これまで勉強してきたことを整理し、あなたの数学力をレベルアップしましょう!
解答はすでにこちらの記事で示しております。
平成30年度(2018)久留米大学医学部一般入試数学[5]
完答必須の複素数平面基本問題です
勉強してきた人ならわかると思いますが,この問題はサービス問題といってもいい,完答しなければならない基本問題です。複素数平面の基本事項のみで解けるし,いざとなったら座標平面でもベクトルでも解くことができます。鼻歌交じりで気持ち良く解いてしまいましょう(笑)。
複素数平面もベクトルも座標平面も同じです
\( \quad \alpha=-1+5i,~\beta=2+3i,~\gamma=3-2i~\)とおく。
- \( \triangle{\mathrm{ABC}}\)の重心を表す複素数は\( \frac{\alpha+\beta+\gamma}{3}\)である。したがって \begin{align*} \frac{\alpha+\beta+\gamma}{3}&=\frac{(-1+5i)+(2+3i)+(3-2i)}{3} \\ &=\frac{4+6i}{3} \\ &=\frac43+2i \quad \cdots \text{(答)} \end{align*}
三角形の重心を表す複素数が,各頂点を表す複素数の和の三分の一,すなわち\( \frac{\alpha+\beta+\gamma}{3}\)であることは基本事項です。
ベクトルで表現すれば\( \frac{\vec{a}+\vec{b}+\vec{c}}{3}\),座標で表現すれば\( \left( \frac{a_1+b_1+c_1}{3},~ \frac{a_2+b_2+c_2}{3} \right) \)であり,全く同じ形であることがわかりますよね。
でも,証明はできるでしょうか?
公式はまず道具として使えることが大事ですが,使えるようになったら次に証明までできるようにしておきましょう。
公式の証明を背景にした問題もありますし,証明を勉強することで,発展問題への対応力がつきます。積極的に取り組みましょう。
複素数と回転・拡大縮小
-
(2)\( \angle{\mathrm{ABC}} \)は複素数平面における偏角\(\mathrm{arg}\frac{\gamma-\beta}{\alpha-\beta}\)を用いて
\begin{align*} \mathrm{arg}\frac{\gamma-\beta}{\alpha-\beta}&=\mathrm{arg}\frac{(3-2i)-(2+3i)}{(-1+5i)-(2+3i)} \\ &=\mathrm{arg}\frac{1-5i}{-3+2i} \\ &=\mathrm{arg}(-1+i) \\ &=\frac34 \pi +2n\pi \quad (n\text{は整数}) \end{align*} したがって\( \angle{\mathrm{ABC}} \)の大きさは \begin{align*} \frac34 \pi \quad \cdots \text{(答)} \end{align*}
\( \mathrm{arg}z \)は,複素数\(z\)の偏角を表します。複素数\( \frac{\gamma-\beta}{\alpha-\beta}\)は,点\(\beta\)を中心に,点\(\alpha\)を点\(\gamma\)まで回転させる複素数です。
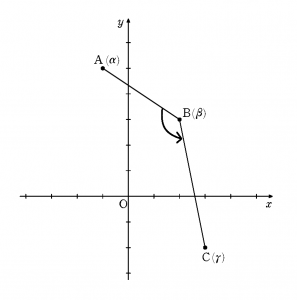
ですから,偏角を\(0\)以上\(2\pi\)未満とすれば,\( \mathrm{arg}\frac{\gamma-\beta}{\alpha-\beta}\)は\( \angle{\mathrm{ABC}} \)に等しくなります。
\( \frac{\gamma-\beta}{\alpha-\beta}\)は,計算すると\( -1+i=\sqrt2 \left( \cos{\frac34\pi}+i \sin{\frac34\pi} \right) \)となりますので,\( \angle{\mathrm{ABC}} \)は\(\frac34 \pi\)となります。
ベクトルと角度といえば内積です
ベクトルで解くならば,内積を利用することになります。
勉強が進んでくると,別の分野だと思っていたものがつながったりするものです。
せっかく勉強するのですから,それを楽しみましょう!
この問題のポイント
振り返ってみましょう。
この問題が解けるかどうかのポイントは、
- 三角形の重心を表す複素数を理解しているか
- 複素数と回転・拡大縮小について理解しているか
- 複素数を極形式で表すことができるか
といったところです。
いずれも基本事項ですので,この機会にしっかり確認しておきましょう。
また,ベクトルの解法も使えることを覚えておきましょう。
※誤植やミスを見つけた方は,ぜひお知らせください。







