[mathjax]
過去問を利用して、久留米大学医学部推薦入試の数学について学びましょう。 令和2年度入試では全部で5問出題されました。 そのうちの2番について、問題と解答を以下にまとめています。 さらに詳しい解説授業は、別の記事にしています。
令和2年度(2020)推薦入試[2]
問題
\(k\)を正の定数とし,座標平面上で表される円\(C:~x^2+y^2-8x-10y+36=0,~\)直線\(l:~2x-y+k=0\)を考える。
- 円\(C\)の中心の座標は\( \left( \boxed{ ケ ~} ,~\boxed{ コ ~} \right) \)であり,半径は\( \sqrt{\boxed{ サ ~}}\)である。
- 直線\(l\)が円\(C\)に接するとき,\(k=\boxed{ シ ~}\)であり,直線\(l\)と円\(C\)の接点の座標は\( \left( \boxed{ ス ~} ,~\boxed{ セ ~} \right) \)である。
久留米推薦(令和2年度入試)
解答
- \(x^2+y^2-8x-10y+36=0\)より\( (x-4)^2+(y-5)^2=5.\)
よって円\(C\)の中心の座標は\( (4,~5),~\)半径は\( \sqrt5 \)である。
- 直線\(l\)が円\(C\)に接するための条件は,円\(C\)の中心\((4,~5)\)と直線\(l\)との距離が\(C\)の半径\(\sqrt5\)に一致するときである。よって
\begin{align*}
\dfrac{|2\cdot4-5+k|}{\sqrt{2^2+(-1)^2}}&=\sqrt5 \\
|k+3|&=5 \\
k&=2,-8
\end{align*}
\(k>0\)より\(k=2. \quad \quad \cdots \text{(答)} \)
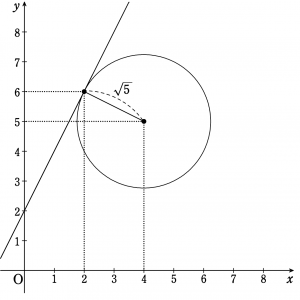
また,接点の座標は下図より\((2,~6). \quad \quad \cdots \text{(答)}\)
さらに詳しい解説授業もあります
この問題でさらに力をつけよう!詳しい解説授業はこちら
※誤植やミスを見つけた方は,ぜひお知らせください。





