過去問を利用して、久留米大学医学部推薦入試の数学について学びましょう。 令和04年度入試では全部で5問出題されました。 そのうちの4番について、問題と解答を以下にまとめています。 さらに詳しい解説授業は、別の記事にしています。
令和04年度(2022)推薦入試[4]
問題
座標空間内に
- 点
- 点
- 点
久留米推薦(令和04年度入試)
解答
- 3点
点
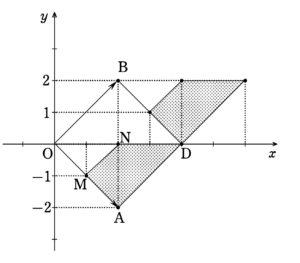 よって,点
よって,点
求める面積 - 点
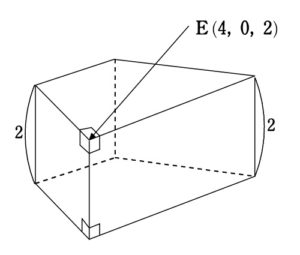
- 点
さらに詳しい解説授業もあります
この問題でさらに力をつけよう!詳しい解説授業はこちら
※誤植やミスを見つけた方は,ぜひお知らせください。






