平成29年度(2017)久留米大学医学部推薦入試数学の過去問と解答（３／５）

[mathjax]

過去問を利用して、久留米大学医学部推薦入試の数学について学びましょう。平成29年度は全部で5問出題されました。そのうちの３番について、問題と解答を以下にまとめています。さらに詳しい解説授業は、別の記事にしています。

平成29年度(2017)推薦入試[３]

平成29年度(2017)推薦入試[３]

問題

2次方程式\(~2x^2-4x-2a+1=0~\)が異なる2つの偶数解をもつ時，\(~a~\)がとりうる値を小さい順に並べた数列\(~{a_n}~\)を考える。次の問いに答えよ。ただし，\(~a~\)は実数，\(~n~\)は正の整数とする。また\(~0~\)は偶数とする。

(1) \( \quad ~a_1~\)の値を求めよ。 (2) \( \quad ~a_n~\)を\(~n~\)を用いて表せ。 (3) \( \quad ~S_n=\displaystyle\sum_{k=1}^{n}{a_k}~\)を求めよ。

久留米推薦（平成29年度）

解答その１

方程式より \[ \begin{align*} x^2-2x-a+\frac{1}{2}=&0 \\ x=&1 \pm \sqrt{1-\left( -a+ \frac{1}{2} \right)} \\ =&1 \pm \sqrt{a+ \frac{1}{2}} \end{align*} \] 与えられた方程式が整数解をもつ条件は\( ~\sqrt{a+ \frac{1}{2}}~ \)が奇数であることである。その奇数を自然数\(k\)を用いて\(~2k-1~\)とし,そのときの\(a\)の値を\(a_k\)とすると \[ \begin{align*} \sqrt{a_k+ \frac{1}{2}}=2k-1 \\ a_k+ \frac{1}{2}=\left(2k-1\right)^2 \\ a_k=4k^2-4k+\frac{1}{2} \end{align*} \] \(~k~\)は自然数であるから，\(~a_k~\)は単調に増加する。

(1)\( \quad a_1=\frac12 \) (2)\( \quad a_n=4n^2-4n+\frac{1}{2}\) (3) \( \quad \begin{align*} S_n=&\displaystyle\sum_{k=1}^{n}{\left( 4k^2-4k+\frac{1}{2} \right)} \\ =&4 \cdot \frac{1}{6}n(n+1)(2n+1)-4 \cdot \frac{1}{2}n(n+1)+\frac{1}{2}n \\ =&\frac{1}{6}n \left\{4(n+1)(2n+1)-12(n+1)+3 \right\} \\ =&\frac{1}{6}n(8n^2-5) \end{align*} \)

解答その２

\(~f(x)=2x^2-4x-2a+1~\)とおくと，\(~y=f(x)~\)の軸は\(~x=1~\)である。 \(~k~\)を自然数として，方程式\(~2x^2-4x-2a+1=0~\)が偶数解\(~x=2k~\)をもつとき，下図よりもう一方の解は\(~x=2-2k~\)である。

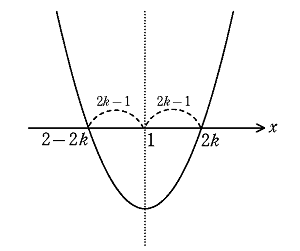
このときの定数\(~a~\)を\(~a_k~\)とすると，次の恒等式が成り立つ。

\[ \begin{align*} 2x^2-4x-2a_k+1=2(x-2k)(x-2+2k) \end{align*} \] 両辺の定数項を比較して \[ \begin{align*} -2a_k+1=&4k(2-2k) \\ a_k=&4k^2-4k+\frac{1}{2} \end{align*} \]

\(~k~\)は自然数であるから，\(~a_k~\)は単調に増加する。

さらに詳しい解説授業もあります

この問題の解説で、さらに力をつけよう！詳しい解説授業はこちら