[mathjax]
この記事には,久留米大学医学部の過去問の詳しい解説が載っています。過去問を通して久留米大学医学部の数学について学べるように,授業のような解説にしています。これまで勉強してきたことを整理し、あなたの数学力をレベルアップしましょう!
解答はすでにこちらの記事で示しております。
平成29年度(2017)久留米大学医学部推薦入試数学[4]
数学Ⅱの「領域と最大最小」問題です。平成28年度(2016)にも出題されている、重要分野です。しっかり勉強して、得意分野にしておきましょう。
まずは方針を立てる
\(x~\)と\(~y~\)についての条件が不等式の形で4つ示されていて,さらに\(~s=\log_{\frac{1}{2}}x\),\(~~t=\log_{\frac{1}{2}}y~\)とおいた後,設問で\(~t-2s~\)などのとりうる値の範囲を問われています。この問題の流れを見ればすぐに,「\(st~\)平面において不等式を満たす領域を示し,最大最小を考える」問題だと気付かなければなりません。
そもそもこの問題は,解きやすいように出題者がヒントを与えてくれています。どこだか分かりますか?
それは,\(~s=\log_{\frac{1}{2}}x\),\(~~t=\log_{\frac{1}{2}}y~\)と書いてあるところです。これは出題者から,「置き換えた文字\(~s~\)と\(~t~\)を用いて表せば解けますよ」という優しいメッセージです。
もし難易度を上げようと思うならば,この\(~s~\)と\(~t~\)を示さず,設問も「\(~s~\)の範囲」は「\( \log_{\frac{1}{2}}x\)の範囲」に,「\(~t-2s~\)のとりうる値の範囲」は「\( \log_{\frac{1}{2}}y -\log_{\frac{1}{2}}x^2\)のとりうる値の範囲」としておけばよいのです。自分で文字を設定する,という手順が増えるため,受験生にとってはハードルが上がってしまいます。
せっくの愛あるメッセージ,見逃さないようにしましょう。
ということで,方針は定まりました。
- \(x~\)と\(~y~\)の不等式を,\(s~\)と\(~t~\)の不等式に置き換える。
- 不等式を満たす領域を\(st\)平面に示す。
- \(st\)平面を用いて最大最小問題を考える
問題を読んだら瞬時に気付くことができるようになりましょう。
「対数をとる」とは何をしているのか
(1) 条件1より\( \quad x \leqq \frac{1}{4}. \) 底を\( ~\frac{1}{2}~\)として両辺の対数をとると \[ \begin{align*} \log_{\frac{1}{2}}x \geqq &\log_{\frac{1}{2}}{\frac{1}{4}} \\ \therefore ~s \geqq &2 \qquad \cdots [1] \end{align*} \]
まず,「対数をとる」ということを,何となくやっている受験生がいますので,ちょっと詳しくお話をします。
例えば,次のような間違いをしたことはありませんか?
\[ \begin{align*} x+y=&100 \\ \log_{10}x +\log_{10}y =&\log_{10}10^2 \\ \log_{10}x +\log_{10}y =&2 \\ \text{※もちろん間違いです!} \end{align*} \]
どこが間違っているか分からない人は,「対数をとる」ということを,「logをつける」とでも解釈しているのでしょう。まったく違いますので,ここで認識を改めましょう。
「対数をとる」とは,与えられた等式の左辺と右辺をそれぞれ真数にもつ(底が等しい)対数をつくっているのです。
その2つの対数は真数が等しいので,もちろん等しいことになります。
先ほどの間違いを訂正すると,次のようになります。
\[ \begin{align*} x+y=&100 \\ \log_{10}(x +y) =&\log_{10}10^2 \\ \log_{10}(x +y) =&2 \\ \text{※こちらは正しい} \end{align*} \]
当たり前と言えば当たり前ですよね。間違えていた人は,2度と間違えないようにしましょう。
さらに,不等式だと注意する点がもう1つあります。
それは,底によって不等号が変わることです。
底を\(~a~\)として,\(a \gt 1 \)のときは \[ x \gt y \\ \log_a x \gt \log_a y \] となりますが,\(0 \lt ~a~ \lt 1\)のときは,以下のように不等号が逆になります。 \[ x \gt y \\ \log_a x \lt \log_a y \]
理由は,\( \log_a x \)のグラフを考えればすぐ分かります。
\( a \gt 1 \)のとき,\( \log_a x \)は増加関数ですが,\( 0 \lt a \lt 1 \)のとき,\( \log_a x \)は減少関数となります。減少関数ということは,\(~x~\)が増加するときに\( \log_a x \)は減少する,ということなので,大小関係から不等号が逆になります。注意しましょう。
領域と最大最小問題の定石
(2) 条件2について,底を\( ~\frac{1}{2}~ \)として両辺の対数をとると \[ \begin{align*} \log_{\frac{1}{2}}y \geqq &\log_{\frac{1}{2}}(16x^2) \\ \log_{\frac{1}{2}}y \geqq &2\log_{\frac{1}{2}}x + \log_{\frac{1}{2}}\left( \frac{1}{2} \right)^{-4} \\[6pt] t \geqq &2s-4 \qquad \cdots [2] \end{align*} \] \(st~ \)平面において,\(~t>0~\)かつ[2]を満たす領域は図の通り。 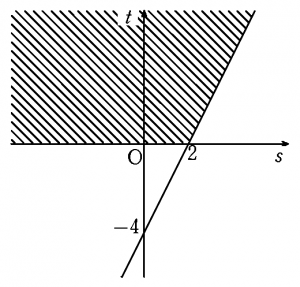
(1)と同じように,条件2について対数をとり,\(s~\)と\(~t~\)についての不等式をつくります。\(~t \gt 0 \)と合わせて領域を示すと図の通りである。横軸は\(~s~\)軸,縦軸は\(~t~\)軸となっていることに注意しよう。
問われているのは\(~t-2s~\)のとりうる値の範囲ですが,このようなとき,\(~t-2s=k~\)とおくのが定石であることは頭に入っていますか?そうすれば,グラフを用いて考えることができます。
\(t=2s+k~\)となるので,傾き\(~2~\), \(~t~\)切片\(~k~\)の直線を表すことがわかります。
\(~k~\)の値が変化すると直線は上下に動きますが,条件式を満たすため,先ほど示した領域と少なくとも1つの点を共有することになります。
よって,\(~t~\)切片が\(−4\)以上となり,すなわち\(~k=t-2s~\)のとりうる値の範囲は\(−4\)以上となります。
直線の傾きに注意しよう
(3),(4)もやっていることは同じです。条件式から\(~s,~t~\)についての不等式をつくり,それを満たす領域を\(~st~\)平面に示します。
(3) 条件3について,底を\( ~\frac{1}{2}~\)として両辺の対数をとると \begin{align*} \log_{\frac{1}{2}}(2^8 \cdot x^2y ) \geqq &\log_{\frac{1}{2}}1 \\ -8+2\log_{\frac{1}{2}}x +\log_{\frac{1}{2}}y \geqq &0 \\ -8+2s+t \geqq &0 \\ \therefore t \geqq &-2s+8 \qquad \cdots [3] \end{align*} 条件4より \begin{align*} \log_{\frac{1}{2}}x + 2\log_{\frac{1}{2}}y \leqq &32 \\ s+2t \leqq &32 \\ \therefore ~t \leqq &-\frac{1}{2}s+16 \qquad \cdots [4] \end{align*} \(st~\)平面において,[1]〜[4]を満たす領域は図の通り。 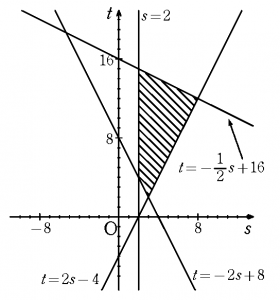
次に,定石通り\(~\log_{\frac{1}{2}}x +\log_{\frac{1}{2}}y=s+t=k~\)とおくことでグラフ化して考えます。直線の傾きがポイントです。
\(s+t=k~\)とおくと\(~t=-s+k\) これは\(~st~\)平面において,傾き\(~-1~\), \(~t~\)切片\(~k~\)の直線を表す。 \(k~\)が最大となるのは,この直線が点\( ~(8,~12)~ \)を通るときであるから,\( ~\log_{\frac{1}{2}}x +\log_{\frac{1}{2}}y=s+t~\)の最大値は\(~8+12=20.\)
最大値を考えるので,傾きが\(~-1~\)である直線\(~t=-s+k\)を上に動かしていきます。
領域の上方には傾きが\(~-\frac12~\)の直線\( ~t=-\frac12x+16 \)がありますので, \(~k~\)が最大となるのは領域の右端の点\( ~(8,~12)~ \)をとおるときであることが分かります。
この点\( ~(8,~12)~ \)は,領域を定めている直線のうちの2本,\( ~t=-\frac12x+16 \)と\(~t=2s-4~\)の交点です。
\(~\log_{\frac{1}{2}}x +\log_{\frac{1}{2}}y~\)の最大値は\(s+t\)の最大値,すなわち\(8+12=20\)となります。
(4)も同じように考えればわかります。
この問題のポイント
振り返ってみましょう。
この問題が解けるかどうかのポイントは、
- \(st~\)平面を利用した領域と最大最小問題であることが見抜ける
- 対数を正確に用いて,\(s~\)と\(~t~\)の不等式をつくることができる
- 定石通り「\(=k\)」とおいて,傾きに注意して直線のグラフで考えることができる
といったところです。苦手だった人はぜひ克服しておきましょう。
克服の手助けが欲しい方はご相談ください






