[mathjax]
 (1)
上図より
\[
\begin{align}
\overrightarrow{\mathrm{OX}}=&\dfrac12\overrightarrow{\mathrm{OB}}+\dfrac12 \overrightarrow{\mathrm{OC}} \\
=&\dfrac12 \overrightarrow{\mathrm{OB}}+\dfrac12 \left( \overrightarrow{\mathrm{OA}} + \overrightarrow{\mathrm{AC}} \right) \\
=&\dfrac12 \vec{b}+ \dfrac12 \left( \vec{a}+ \dfrac13 \vec{b} \right) \\
=& \dfrac12 \vec{a}+ \dfrac23 \vec{b}
\end{align}
\]
したがって
\[
\begin{align*}
\overrightarrow{\rm{AX}}=&\overrightarrow{\rm{OX}}-\overrightarrow{\rm{OA}} \\
=&\left( \dfrac{1}{2}\vec{a}+\dfrac{2}{3}\vec{b} \right)-\vec{a} \\
=&-\dfrac{1}{2}\vec{a}+\dfrac{2}{3}\vec{b} \quad \cdots \text{(答)}
\end{align*}
\]
(2)
\[
\begin{align*}
\overrightarrow{\rm{YX}}=&\overrightarrow{\rm{OX}}-\overrightarrow{\rm{OY}} \\
=&\left( \dfrac{1}{2}\vec{a}+\dfrac{2}{3}\vec{b} \right)-\dfrac{4}{9}\vec{b} \\
=&\dfrac{1}{2}\vec{a}+\dfrac{2}{9}\vec{b} \quad \cdots \text{(答)}
\end{align*}
\]
(3)
\( \angle {\rm{AYX}}=\dfrac{\pi}{2}~\)のとき,\(~\rm{AY} \perp \rm{YX}\)すなわち\(~\overrightarrow{\rm{AY}} \cdot \overrightarrow{\rm{YX}}=0~\)である。\(~\overrightarrow{\rm{AY}}=\overrightarrow{\rm{OY}}-\overrightarrow{\rm{OA}}=-\vec{a}+\dfrac{4}{9}\vec{b}~\)であるから
\[
\begin{align*}
\left( -\vec{a}+\dfrac{4}{9}\vec{b} \right)\cdot \left( \dfrac{1}{2}\vec{a}+\dfrac{2}{9}\vec{b} \right)=&0 \\
-\dfrac12 \left( \vec{a}-\dfrac{4}{9}\vec{b} \right)\cdot \left( \vec{a}+\dfrac{4}{9}\vec{b} \right)=&0 \\
|\vec{a}|^2-\dfrac{16}{81}|\vec{b}|^2=&0
\end{align*}
\]
\( |\vec{b}|=3r\)なので
\[
\begin{align*}
|\vec{a}|^2-\dfrac{16}{81}(3r)^2=&0 \\
|\vec{a}|^2=&\dfrac{16}{9}r^2
\end{align*}
\]
したがって
\[
\mathrm{OA}=|\vec{a}|=\dfrac{4}{3}r \quad \cdots \text{(答)}
\]
(1)
上図より
\[
\begin{align}
\overrightarrow{\mathrm{OX}}=&\dfrac12\overrightarrow{\mathrm{OB}}+\dfrac12 \overrightarrow{\mathrm{OC}} \\
=&\dfrac12 \overrightarrow{\mathrm{OB}}+\dfrac12 \left( \overrightarrow{\mathrm{OA}} + \overrightarrow{\mathrm{AC}} \right) \\
=&\dfrac12 \vec{b}+ \dfrac12 \left( \vec{a}+ \dfrac13 \vec{b} \right) \\
=& \dfrac12 \vec{a}+ \dfrac23 \vec{b}
\end{align}
\]
したがって
\[
\begin{align*}
\overrightarrow{\rm{AX}}=&\overrightarrow{\rm{OX}}-\overrightarrow{\rm{OA}} \\
=&\left( \dfrac{1}{2}\vec{a}+\dfrac{2}{3}\vec{b} \right)-\vec{a} \\
=&-\dfrac{1}{2}\vec{a}+\dfrac{2}{3}\vec{b} \quad \cdots \text{(答)}
\end{align*}
\]
(2)
\[
\begin{align*}
\overrightarrow{\rm{YX}}=&\overrightarrow{\rm{OX}}-\overrightarrow{\rm{OY}} \\
=&\left( \dfrac{1}{2}\vec{a}+\dfrac{2}{3}\vec{b} \right)-\dfrac{4}{9}\vec{b} \\
=&\dfrac{1}{2}\vec{a}+\dfrac{2}{9}\vec{b} \quad \cdots \text{(答)}
\end{align*}
\]
(3)
\( \angle {\rm{AYX}}=\dfrac{\pi}{2}~\)のとき,\(~\rm{AY} \perp \rm{YX}\)すなわち\(~\overrightarrow{\rm{AY}} \cdot \overrightarrow{\rm{YX}}=0~\)である。\(~\overrightarrow{\rm{AY}}=\overrightarrow{\rm{OY}}-\overrightarrow{\rm{OA}}=-\vec{a}+\dfrac{4}{9}\vec{b}~\)であるから
\[
\begin{align*}
\left( -\vec{a}+\dfrac{4}{9}\vec{b} \right)\cdot \left( \dfrac{1}{2}\vec{a}+\dfrac{2}{9}\vec{b} \right)=&0 \\
-\dfrac12 \left( \vec{a}-\dfrac{4}{9}\vec{b} \right)\cdot \left( \vec{a}+\dfrac{4}{9}\vec{b} \right)=&0 \\
|\vec{a}|^2-\dfrac{16}{81}|\vec{b}|^2=&0
\end{align*}
\]
\( |\vec{b}|=3r\)なので
\[
\begin{align*}
|\vec{a}|^2-\dfrac{16}{81}(3r)^2=&0 \\
|\vec{a}|^2=&\dfrac{16}{9}r^2
\end{align*}
\]
したがって
\[
\mathrm{OA}=|\vec{a}|=\dfrac{4}{3}r \quad \cdots \text{(答)}
\]
過去問を利用して、久留米大学医学部推薦入試の数学について学びましょう。 平成28年度は全部で5問出題されました。 そのうちの3番について、問題と解答を以下にまとめています。 さらに詳しい解説授業は、別の記事にしています。
平成28年度(2016)推薦入試[3]
問題
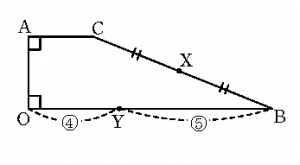
台形AOBCは,辺ACと辺OBが平行で,\(~\angle {\rm{AOB}}=\dfrac{\pi}{2}~\)となっている。辺OBは辺ACの3倍の長さとなっている。辺BCの中点をX,辺OBを4:5に内分する点をYとする。辺ACの長さを\(~r~\)とおき,\(~\overrightarrow{\rm{OA}}=\vec{a},~\overrightarrow{\rm{OB}}=\vec{b}~\)とおく。
- \( \overrightarrow{\rm{AX}}~\)を\(~\vec{a},~\vec{b}~\)を用いて表せ。
- \( \overrightarrow{\rm{YX}}~\)を\(~\vec{a},~\vec{b}~\)を用いて表せ。
- \( \angle {\rm{AYX}}=\dfrac{\pi}{2}~\)となった場合,辺OAの長さはいくらか。
久留米推薦(平成28年度)
解答
 (1)
上図より
\[
\begin{align}
\overrightarrow{\mathrm{OX}}=&\dfrac12\overrightarrow{\mathrm{OB}}+\dfrac12 \overrightarrow{\mathrm{OC}} \\
=&\dfrac12 \overrightarrow{\mathrm{OB}}+\dfrac12 \left( \overrightarrow{\mathrm{OA}} + \overrightarrow{\mathrm{AC}} \right) \\
=&\dfrac12 \vec{b}+ \dfrac12 \left( \vec{a}+ \dfrac13 \vec{b} \right) \\
=& \dfrac12 \vec{a}+ \dfrac23 \vec{b}
\end{align}
\]
したがって
\[
\begin{align*}
\overrightarrow{\rm{AX}}=&\overrightarrow{\rm{OX}}-\overrightarrow{\rm{OA}} \\
=&\left( \dfrac{1}{2}\vec{a}+\dfrac{2}{3}\vec{b} \right)-\vec{a} \\
=&-\dfrac{1}{2}\vec{a}+\dfrac{2}{3}\vec{b} \quad \cdots \text{(答)}
\end{align*}
\]
(2)
\[
\begin{align*}
\overrightarrow{\rm{YX}}=&\overrightarrow{\rm{OX}}-\overrightarrow{\rm{OY}} \\
=&\left( \dfrac{1}{2}\vec{a}+\dfrac{2}{3}\vec{b} \right)-\dfrac{4}{9}\vec{b} \\
=&\dfrac{1}{2}\vec{a}+\dfrac{2}{9}\vec{b} \quad \cdots \text{(答)}
\end{align*}
\]
(3)
\( \angle {\rm{AYX}}=\dfrac{\pi}{2}~\)のとき,\(~\rm{AY} \perp \rm{YX}\)すなわち\(~\overrightarrow{\rm{AY}} \cdot \overrightarrow{\rm{YX}}=0~\)である。\(~\overrightarrow{\rm{AY}}=\overrightarrow{\rm{OY}}-\overrightarrow{\rm{OA}}=-\vec{a}+\dfrac{4}{9}\vec{b}~\)であるから
\[
\begin{align*}
\left( -\vec{a}+\dfrac{4}{9}\vec{b} \right)\cdot \left( \dfrac{1}{2}\vec{a}+\dfrac{2}{9}\vec{b} \right)=&0 \\
-\dfrac12 \left( \vec{a}-\dfrac{4}{9}\vec{b} \right)\cdot \left( \vec{a}+\dfrac{4}{9}\vec{b} \right)=&0 \\
|\vec{a}|^2-\dfrac{16}{81}|\vec{b}|^2=&0
\end{align*}
\]
\( |\vec{b}|=3r\)なので
\[
\begin{align*}
|\vec{a}|^2-\dfrac{16}{81}(3r)^2=&0 \\
|\vec{a}|^2=&\dfrac{16}{9}r^2
\end{align*}
\]
したがって
\[
\mathrm{OA}=|\vec{a}|=\dfrac{4}{3}r \quad \cdots \text{(答)}
\]
(1)
上図より
\[
\begin{align}
\overrightarrow{\mathrm{OX}}=&\dfrac12\overrightarrow{\mathrm{OB}}+\dfrac12 \overrightarrow{\mathrm{OC}} \\
=&\dfrac12 \overrightarrow{\mathrm{OB}}+\dfrac12 \left( \overrightarrow{\mathrm{OA}} + \overrightarrow{\mathrm{AC}} \right) \\
=&\dfrac12 \vec{b}+ \dfrac12 \left( \vec{a}+ \dfrac13 \vec{b} \right) \\
=& \dfrac12 \vec{a}+ \dfrac23 \vec{b}
\end{align}
\]
したがって
\[
\begin{align*}
\overrightarrow{\rm{AX}}=&\overrightarrow{\rm{OX}}-\overrightarrow{\rm{OA}} \\
=&\left( \dfrac{1}{2}\vec{a}+\dfrac{2}{3}\vec{b} \right)-\vec{a} \\
=&-\dfrac{1}{2}\vec{a}+\dfrac{2}{3}\vec{b} \quad \cdots \text{(答)}
\end{align*}
\]
(2)
\[
\begin{align*}
\overrightarrow{\rm{YX}}=&\overrightarrow{\rm{OX}}-\overrightarrow{\rm{OY}} \\
=&\left( \dfrac{1}{2}\vec{a}+\dfrac{2}{3}\vec{b} \right)-\dfrac{4}{9}\vec{b} \\
=&\dfrac{1}{2}\vec{a}+\dfrac{2}{9}\vec{b} \quad \cdots \text{(答)}
\end{align*}
\]
(3)
\( \angle {\rm{AYX}}=\dfrac{\pi}{2}~\)のとき,\(~\rm{AY} \perp \rm{YX}\)すなわち\(~\overrightarrow{\rm{AY}} \cdot \overrightarrow{\rm{YX}}=0~\)である。\(~\overrightarrow{\rm{AY}}=\overrightarrow{\rm{OY}}-\overrightarrow{\rm{OA}}=-\vec{a}+\dfrac{4}{9}\vec{b}~\)であるから
\[
\begin{align*}
\left( -\vec{a}+\dfrac{4}{9}\vec{b} \right)\cdot \left( \dfrac{1}{2}\vec{a}+\dfrac{2}{9}\vec{b} \right)=&0 \\
-\dfrac12 \left( \vec{a}-\dfrac{4}{9}\vec{b} \right)\cdot \left( \vec{a}+\dfrac{4}{9}\vec{b} \right)=&0 \\
|\vec{a}|^2-\dfrac{16}{81}|\vec{b}|^2=&0
\end{align*}
\]
\( |\vec{b}|=3r\)なので
\[
\begin{align*}
|\vec{a}|^2-\dfrac{16}{81}(3r)^2=&0 \\
|\vec{a}|^2=&\dfrac{16}{9}r^2
\end{align*}
\]
したがって
\[
\mathrm{OA}=|\vec{a}|=\dfrac{4}{3}r \quad \cdots \text{(答)}
\]
さらに詳しい解説授業もあります
この問題でさらに力をつけよう!詳しい解説授業はこちら






