[mathjax]
この記事には,久留米大学医学部の過去問の詳しい解説が載っています。過去問を通して久留米大学医学部の数学について学べるように,授業のような解説にしています。これまで勉強してきたことを整理し、あなたの数学力をレベルアップしましょう!
解答はすでにこちらの記事で示しております。
平成30年度(2018)久留米大学医学部推薦入試数学[1]
公式の\( n \) はすべての自然数
\( (1),~(2) \) は公式を確認するだけの基本問題です。落とすわけにはいきません。\( n \) はすべての自然数ですから,必要に応じて自然数を代入することで式を立てましょう。
(1)\( \quad \)初項を\( a_1,~\)公差を\(d\)とすると
\begin{align*} a_1+19d&=30 \quad \quad \cdots [1] \\ a_1+39d&=-90 \quad \cdots [2] \end{align*}[2]-[1]より
\begin{align*} 20d&=-120 \\ d&=-6 \end{align*} [1]より \begin{align*} a_1+19\cdot(-6)&=30 \\ a_1&=144 \end{align*} したがって \begin{align*} a_n&=144-6(n-1) \\ &=-6n+150 \quad \cdots \text{(答)} \end{align*}答が出たら,\( n=1,~2 \)などを代入することで計算ミスをしていないか確認しておきましょう。ちょっとしたことですが,日ごろから習慣づけておくとかなりのミスを減らすことができます。
(2)\( \quad\)初項から第\(n\)項までの和は
\begin{align*} S_n=&\displaystyle \frac {n(a_1+a_n)}{2} \\ =&\displaystyle \frac{n\left\{ 144+(-6n+150) \right\}}{2} \\ =&3n(49-n) \quad \cdots \text{(答)} \end{align*}等差数列の和の公式は,\( S_n=\displaystyle \frac {n(a_1+a_n)}{2} \)です。教科書にはもう一つ,\( S_n=\displaystyle \frac{n}{2} \left\{ 2a_1+(n-1)d \right\} \)が載っているので,こちらも合わせて二つとも覚えている人は多いでしょう。ただこちらの式は,前の式と一般項の公式を使えば作り出すことができます。 \begin{align*} S_n&=\displaystyle \frac {n(a_1+a_n)}{2} \\ &=\displaystyle \frac {n \left\{ a_1+a_1+(n-1)d \right\}}{2} \\ &=\displaystyle \frac{n}{2} \left\{ 2a_1+(n-1)d \right\} \end{align*} 丸暗記では忘れてしまいます。このように公式を作り出す過程をおろそかにしないで,何度でもやりましょう。おのずと記憶に残り,絶対に忘れない財産となります。
和の式に着目するか,一般項に着目するか
(3)を解くにあたって,解法は2つあります。和の最大値を求めるために,和そのものに着目するのか,一般項に着目するのか,の2通りです。まずはおススメの,一般項に着目する解法です。
\begin{align*} -6n+150 &\geqq 0 \\ n &\leqq 25 \end{align*}
まずは,\( a_n \geqq 0 \)として,\(a_n\)が0以上となる項について調べています。なぜでしょうか。
\( S_n \)は,初項から第\(n\)項までの和です。正の項であれば足せば足すほど\(S_n\)は大きくなりますが,負の項を足していけば\(S_n\)は小さくなります。
そこで,数列\( \left\{a_n \right\} \)のどこに正の項が並んでいるのかを調べるのです。
\(\quad a_n \geqq 0 \) を満たすのは\( ~n \leqq 25~\) です。ということは,\(~a_1 \)から\(~a_{24}~\)までは正の項,\(~a_{25}=0~\),\(~a_{26},~a_{27}~\)以降は負の項だと分かります。
正の項は足せば足すほど\(~S_n~\)が大きくなるのですから,\(S_1~\)より\(~S_2~\),\(S_2~\)より\(~S_3~,~\cdots \)とどんどん大きくなります。
ただし,それは\(~S_{24}~\)まで。第25項\(a_{25} \)は\(0\)なので,\(~S_{24}~=S_{25}~\)となります。ここが\( S_n \)が最大となるところであり,これ以降,\(S_{26},~S_{27},~\cdots \)と\( ~n~\)が大きくなるほど\(~S_n~\)は小さくなっていきます。
したがって,\( S_n \)が最大となるのは\( n=24,~25 \)のときであるとわかるのです。
和が最大となるときを調べようと思えば,\(~S_n~\)の式を調べようと思うのが自然だと思います。でもこの解法は,和を調べずに一般項を調べるところにポイントがあります。
ちょっと数学的センスを感じませんか(笑)?
数学が苦手な人は,とにかく教えられた解法を覚えようとする傾向にあります。意味もなく単に覚えなければならないのは苦痛です。せっかくなら,「解法の視点がユニークだなあ」などとちょっとだけ感動しながら勉強すると,数学が楽しくなるかもしれませんよ。
性格がとても素直な人のために(笑),素直に和の式を調べる解法を示しておきましょう。
\(f(x)=3x \left(49-x \right)\)とおくと,放物線\(~y=f(x) \)上の\(~x=1,~2,~\cdots ,~n~ \)である点の\(~y~\)座標\(~f(1),~f(2),~\cdots ,~f(n)~ \)がそれぞれ\(~S_1,~S_2,~\cdots ,~S_n~\)となる。
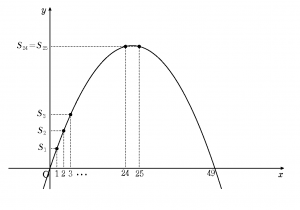
放物線の軸の方程式は\(~x=\frac{49}{2}=24+\frac12~\)であるから,\(S_n~\)が最大となるのは\(~n=24,~25~\)のときである。(後略)
こちらの解法を使った場合でも,上記のように考えればさほど問題はありません。ただし,2次関数を見ると,とにかく平方完成をしようとする受験生もいます。そんな人はちょっと面倒な計算で時間をロスしたかもしれません。計算量が多くなるばかりで何も得するものはないので,平方完成しなくてもいい場合はなるべく避けましょう。
この問題のポイント
振り返ってみましょう。
この問題が解けるかどうかのポイントは、
- 等差数列の公式を正しく用いることができるか。
- 等差数列の和の最大値を求めるために,一般項の正負を調べて解くことができるか。
- 等差数列の和の最大値を求めるために,和の式からグラフを用いて解くことができるか
といったところです。似た問題は,市販の問題集にもよく載っていますので,気になる人は見つけて練習を積んでおきましょう。






