過去問を利用して、久留米大学医学部推薦入試の数学について学びましょう。 令和3年度(2021)の推薦入試では,全部で5問出題されました。 そのうちの1番について、問題と解答を以下にまとめています。 さらに詳しい解説授業は、別の記事にしています。
令和3年度(2021)久留米大学医学部推薦入試[1/5]
問題
全体集合\(U\)に対し,どの集合も空集合でない4つの部分集合\(A,~B,~C,~D~\)があり,これらの4つの集合について次の6つのことがわかっている。また,集合\(C\)の補集合を\(\overline{C}\)とする。
- 集合\(A\)の要素でないものは集合\(B\)の要素でない。
- 集合\(B\)の要素でないものでも集合\(C\)の要素となるものが存在する。
- 集合\(B\)と集合\(C\)の両方の要素であるものが存在する。
- 集合\(C\)の要素はすべて集合\(A\)の要素である。
- 集合\(D\)の要素で集合\(C\)の要素となるものは存在しない。
- 集合\(D\)の要素はすべて集合\(B\)の要素である。
- 次の\(\fbox{ ① }\)〜\(\fbox{ ⑤ }\)に当てはまるものを,下の\(0\)〜\(2\)のうちから一つずつ選べ。ただし,同じものを繰り返し選んでもよい。
- 命題「\(B \subset A\)である」は\(\fbox{ ① }\)。
- 命題「\(B \subset C\)である」は\(\fbox{ ② }\)。
- 命題「\(B \cap D \subset A\)である」は\(\fbox{ ③ }\)。
- 命題「\(C \cap D \neq \phi\)である」は\(\fbox{ ④ }\)。
- 命題「\(\overline{C \cup \overline{D}} \subset (A \cap B)\)である」は\(\fbox{ ⑤ }\)。
- 次の\(\fbox{ ⑥ } , ~\fbox{ ⑦ }\)に当てはまるものを,下の\(0\)〜\(3\)のうちから一つずつ選べ。ただし,同じものを繰り返し選んでもよい。
- 集合\(C\)の要素であることは,集合\(A\)の要素であるための\(\fbox{ ⑥ }\)。
- 集合\(A\)の要素であることは,集合\(A\)以外の集合の要素であるための\(\fbox{ ⑦ }\)。
- \(0~\)必要十分条件である
- \(1~\)十分条件であるが,必要条件ではない
- \(2~\)必要条件であるが,十分条件ではない
- \(3~\)必要条件でも十分条件でもない
久留米推薦(令和3年度)
解答
「集合\(A\)の要素でないものは集合\(B\)の要素でない」より\(A \supset B \)
「集合\(B\)の要素でないものでも集合\(C\)の要素となるものが存在する」より\( \overline{B}\cap C \neq \phi \)
「集合\(B\)と集合\(C\)の両方の要素であるものが存在する」より\( B \cap C \neq \phi \)
「集合\(C\)の要素はすべて集合\(A\)の要素である。」より\(A \supset C\)
「集合\(D\)の要素で集合\(C\)の要素となるものは存在しない」より\(D \cap C = \phi \)
「集合\(D\)の要素はすべて集合\(B\)の要素である」より\( D \subset B \)
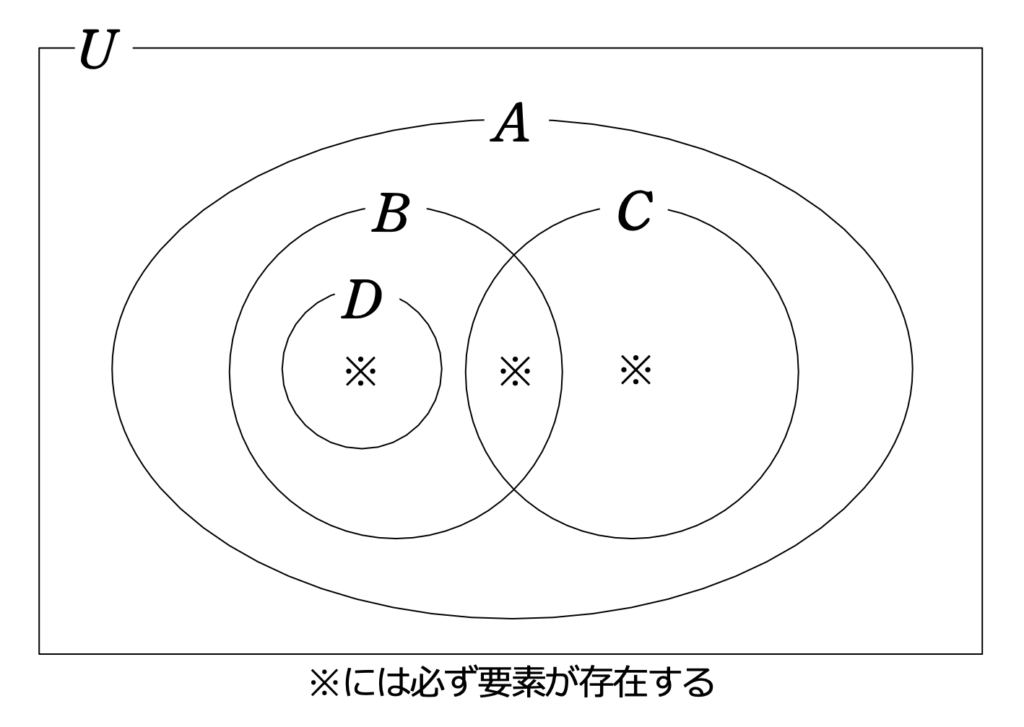
(1)
ベン図より
- 命題「\(B \subset A\)である」は真。よって\(0 \cdots \text{(答)} \)
- >命題「\(B \subset C\)である」は偽。よって\(1 \cdots \text{(答)} \)
- 命題「\(B \cap D \subset A\)である」は真。よって\(0 \cdots \text{(答)} \)
- 命題「\(C \cap D \neq \phi\)である」は偽。よって\(1 \cdots \text{(答)}\)
- 命題「\(\overline{C \cup \overline{D}} \subset (A \cap B)\)である」は「\((\overline{C} \cap D) \subset (A \cap B)\)である」と同値であり,真。よって\(0 \cdots \text{(答)} \)
(2)
- 集合\(C\)の要素であることは,集合\(A\)の要素であるための,十分条件であるが必要条件ではない(\(A=C\)となることはない)。よって\(1 \cdots \text{(答)} \)
- 集合\(A\)の要素であることは,集合\(A\)以外の集合の要素であるための必要条件である。十分条件かどうかは判断できないが\((A=(B\cup C \cup D)\)の可能性もある)出題者が用意した答えは,おそらく\(2 \cdots \text{(答)} \) 。
さらに詳しい解説授業もあります
この問題でさらに力をつけよう!詳しい解説授業はこちら






