過去問を利用して、久留米大学医学部推薦入試の数学について学びましょう。 令和04年度入試では全部で5問出題されました。 そのうちの3番について、問題と解答を以下にまとめています。 さらに詳しい解説授業は、別の記事にしています。
令和04年度(2022)推薦入試[3]
問題
放物線\( y=\dfrac{\sqrt2}{4}x^2~\)と円\(C: x^2+(y-a)^2=8~\)が2点で接している。ただし,\( a \)は実数の定数とする。
- \(a=\boxed{\Large\phantom{ppp}}\)であり,2つの接点のうち\(x\)座標が正である座標は\(\boxed{\Large\phantom{ppp}}\)である。さらに,放物線\( y=\dfrac{\sqrt2}{4}x^2~\)と円\(C\)とで囲まれた部分の面積は\(\dfrac{\boxed{\Large\phantom{ppp}}}{3}\)である。
- 放物線\(y=mx^2+n~ (m<0)\)と円\(C\)も2点で接し,その接点をP, Q, とする。円\(C\)の中心をTとするとき,∠PTQ=\(90^{\circ}\)となるのは, \(m=\boxed{\Large\phantom{ppp}},~ n=\dfrac{\boxed{\Large\phantom{ppp}}}{2}\)のときである。
久留米推薦(令和04年度入試)
解答
- \( y=\frac {\sqrt2}{4}x^2\)と\(x^2+(y-a)^2=8\)より\(x\)を消去して、
\begin{align*}
2\sqrt2 y+(y-a)^2=& 8 \\
y^2-2(a-\sqrt2)y +a^2-8 =& 0
\end{align*}
放物線と円が2点で接する条件は,この\(y\)についての2次方程式が正の重解をもつことである。判別式を\(D\)として
\begin{align*}
D=& 0 \\
(a-\sqrt2)^2-a^2+8=& 0 \\
\therefore a=\frac{5\sqrt2}{2} \quad \cdots \text{(答)}
\end{align*}
このとき,重解は\(y=a-\sqrt2=\frac{5\sqrt2}{2}-\sqrt2=\frac{3\sqrt2}{2} \)であり,正の数である。
\(x\)座標は\(x^2=2\sqrt2 y=2\sqrt2 \times \frac{3\sqrt2}{2}=6\)より\(x=\pm \sqrt6.\)
よって2つの接点のうち\(x\)座標が正である座標は\( \left( \sqrt{6},~ \frac{3\sqrt{2}}{2} \right) \quad \cdots \text{(答)} \)
放物線と円で囲まれた部分の面積\(S\)は,下の図より \begin{align*} S=& \frac16 \cdot \frac{\sqrt{2}}{4} \left\{ \sqrt6 -(-\sqrt6)\right\}^3 + \sqrt2 \times \sqrt6 -\frac12 \cdot (2\sqrt2)^2 \cdot \frac{2\pi}{3} \\ =& 6\sqrt3 -\frac{8\pi}{3} \quad \cdots \text{(答)} \end{align*}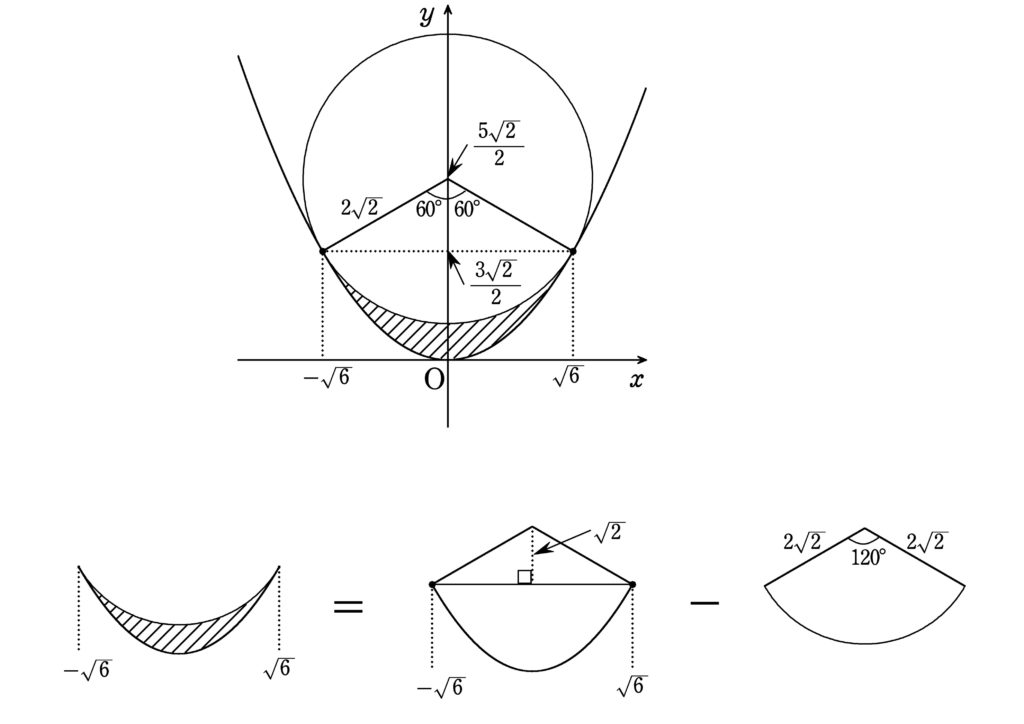
-
∠PTQ=90°より,直線TP, TQの傾きは\(-1\)と\(1\)である。線分TP\(,~\)TQの長さは円の半径\(2\sqrt2\)に等しいので,P\(,~\)Tの\(~x~\)座標は\(-2\)と\(2\)であり,\(y~\)座標は\(\frac{5\sqrt2}{2}+2\)とわかる。
\(y=mx^2+n\)は,\(x=2\)の点で円と接しており,この点における接線の傾きは\(-1\)である。\(y’=2mx\)であるから
\begin{align*} 2m \times 2 =& -1 \\ m=& -\frac14 \quad \cdots \text{(答)} \end{align*}{} 放物線の式を\(y=-\frac14x^2+n\)として,通る点の座標\(x=\pm 2,~y=\frac{5\sqrt2}{2}+2 \)を代入して \begin{align*} \frac{5\sqrt2}{2}+2=& -\frac14 \cdot 4 +n \\ n=& \frac{5\sqrt2+6}{2} \quad \cdots \text{(答)} \end{align*}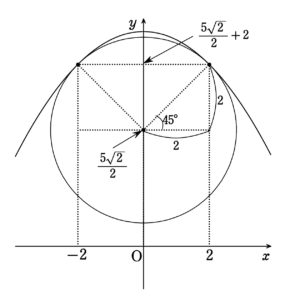
さらに詳しい解説授業もあります
この問題でさらに力をつけよう!詳しい解説授業はこちら
※誤植やミスを見つけた方は,ぜひお知らせください。






