過去問を利用して、久留米大学医学部推薦入試の数学について学びましょう。 令和05年度入試では全部で4問出題されました。 そのうちの3番について、問題と解答を以下にまとめています。 さらに詳しい解説授業は、別の記事にしています。
令和05年度(2023)推薦入試[3]
問題
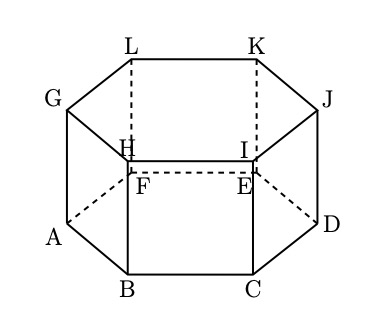
図のように,すべての辺の長さが1であるような正六角柱ABCDEF-GHIJKLがあり,3点A, I, Kを含む平面を\(\alpha\) とする。
\(\overrightarrow{\textrm{AB}}=\vec{p},~\overrightarrow{\textrm{AF}}=\vec{q},~\overrightarrow{\textrm{AG}}=\vec{r}\)とするとき,
(1) \(\vec{p}\cdot \vec{q}=\boxed{~~12 ~~} ,~\vec{p}\cdot \vec{r}=\vec{q}\cdot \vec{r}=\boxed{~~ 13 ~~} \)である。
(2) ベクトル\(\overrightarrow{\textrm{AK}},~\overrightarrow{\textrm{AI}}\)は\(\vec{p},~\vec{q},~\vec{r}\)を用いて
\begin{align*}
\overrightarrow{\textrm{AK}}=\boxed{~~14~~},~\overrightarrow{\textrm{AI}}=\boxed{~~15~~}
\end{align*}
と表せる。ただし,\(\boxed{~~14~~},~\boxed{~~15~~}\)に当てはまるものを下の\(0.\)〜\(8.\)の中から1つずつ選べ。
- \(\vec{p}+\vec{q}+\vec{r}\)
- \(\vec{p}+\vec{q}-\vec{r}\)
- \(\vec{p}-\vec{q}-\vec{r}\)
- \(2\vec{p}+\vec{q}+\vec{r}\)
- \(\vec{p}+2\vec{q}+\vec{r}\)
- \(\vec{p}+\vec{q}+2\vec{r}\)
- \(2\vec{p}+2\vec{q}-\vec{r}\)
- \(2\vec{p}-2\vec{q}+\vec{r}\)
- \(2\vec{p}-2\vec{q}-\vec{r}\)
また,直線\(\textrm{LC}\)と平面\(\alpha\)の交点を\(\textrm{P}\)とすると,\(\textrm{P}\)は平面\(\alpha\)上にあるから,実数\(s,~t\)を用いて\(\overrightarrow{\textrm{AP}}=s\overrightarrow{\textrm{AK}}+t\overrightarrow{\textrm{AI}}\)とおけるので,
\begin{align*}
\overrightarrow{\textrm{AP}}=\boxed{~~16~~}\vec{p}+\boxed{~~17~~}\vec{q}+\boxed{~~18~~}\vec{r}
\end{align*}
と表せる。ただし,\(\boxed{~~16~~},~\boxed{~~17~~},~\boxed{~~18~~}\)に当てはまるものを下の\(0.\)〜\(7.\)の中から1つずつ選べ。同じものを繰り返し選んでもよいものとする。
- \(s+t\)
- \(s-t\)
- \(2s+t\)
- \(2s-t\)
- \(s+2t\)
- \(s-2t\)
- \(2s+2t\)
- \(2s-2t\)
一方,ベクトル\(\overrightarrow{\textrm{AL}},~\overrightarrow{\textrm{LC}}~\)は\(~\vec{p},~\vec{q},~\vec{r}~\)を用いて
\begin{align*}
\overrightarrow{\textrm{AL}}=\boxed{~~19~~},~\overrightarrow{\textrm{LC}}=\boxed{~~20~~}
\end{align*}
と表せる。
したがって,\(\overrightarrow{\textrm{AP}}~\)を\(~\overrightarrow{\textrm{AK}}~\)と\(~\overrightarrow{\textrm{AI}}~\)を用いて表すと,
\begin{align*}
\overrightarrow{\textrm{AP}}=\boxed{~~21~~}\overrightarrow{\textrm{AK}}+\boxed{~~22~~}\overrightarrow{\textrm{AI}}
\end{align*}
である。ただし,\(\boxed{~~21~~}\)と\(\boxed{~~22~~}\)には\(s,~t\)を用いず,既約分数を用いて答えよ。
また,直線\(\textrm{AP}\)と直線\(\textrm{KI}\)の交点を\(\textrm{Q}\)とすると,点\(\textrm{Q}\)は\(\boxed{~~23~~}\)である。ただし,\(\boxed{~~23~~}\)に当てはまるものを下の\(0.\)〜\(3.\)の中から1つ選べ。
- 線分\(\textrm{KI}\)を\(2:3\)に内分する点
- 線分\(\textrm{KI}\)を\(3:2\)に内分する点
- 線分\(\textrm{KI}\)を\(1:2\)に内分する点
- 線分\(\textrm{KI}\)を\(2:1\)に内分する点
久留米推薦(令和05年度入試)
解答
\[
\vec{p}\cdot \vec{q}=|\vec{p}||\vec{q}|\cos \frac{2\pi}{3}=1 \cdot 1 \cdot \left( -\frac12 \right)=-\frac12. \quad \cdots \text{(答)}
\]
\( \vec{p} \perp \vec{r},~ \vec{q} \perp \vec{r}\)なので
\[
\vec{p} \cdot \vec{r}=\vec{q} \cdot \vec{r}=0. \quad \cdots \text{(答)}
\]
\begin{align*}
\overrightarrow{\textrm{AK}}= & \overrightarrow{\textrm{AF}}+\overrightarrow{\textrm{FE}}+\overrightarrow{\textrm{EK}} \\
= & \overrightarrow{\textrm{AF}}+\left( \overrightarrow{\textrm{AB}}+\overrightarrow{\textrm{AF}} \right) +\overrightarrow{\textrm{AG}} \\
= & \vec{p}+2\vec{q}+\vec{r} \quad \therefore 4. \quad \cdots \text{(答)}
\end{align*}
\begin{align*}
\overrightarrow{\textrm{AI}}= & \overrightarrow{\textrm{AB}}+\overrightarrow{\textrm{BC}}+\overrightarrow{\textrm{CI}} \\
= & \overrightarrow{\textrm{AB}}+\left( \overrightarrow{\textrm{AB}}+\overrightarrow{\textrm{AF}} \right)+\overrightarrow{\textrm{AG}} \\
= & 2\vec{p}+\vec{q}+\vec{r} \quad \therefore 3. \quad \cdots \text{(答)}
\end{align*}
\begin{align*}
\overrightarrow{\textrm{AP}}= & s\overrightarrow{\textrm{AK}}+t\overrightarrow{\textrm{AI}} \\
= & s \left( \vec{p}+ 2\vec{q}+\vec{r} \right) + t \left( 2\vec{p}+ \vec{q}+\vec{r} \right)\\
= & (s+2t)\vec{p}+(2s+t)\vec{q}+(s+t)\vec{r} \quad \cdots [1]
\end{align*}
よって \( \qquad 4,~2,~0 \quad \cdots \text{(答)} \)
また一方,
\begin{align*}
\overrightarrow{\textrm{AL}}= & \overrightarrow{\textrm{AF}}+\overrightarrow{\textrm{FL}} \\
= & \overrightarrow{\textrm{AF}}+\overrightarrow{\textrm{AG}} \\
= & \vec{q}+\vec{r} \quad \cdots \text{(答)}
\end{align*}
\begin{align*}
\overrightarrow{\textrm{LC}}= & \overrightarrow{\textrm{LI}}+\overrightarrow{\textrm{IC}} \\
= & 2\overrightarrow{\textrm{AB}}+\overrightarrow{\textrm{GA}} \\
= & 2\vec{p}-\vec{r} \quad \cdots \text{(答)}
\end{align*}
点\(\textrm{P}\)は直線\(\textrm{LC}\)上にあるので,実数\(u\)を用いて
\begin{align*}
\overrightarrow{\textrm{AP}}= & \overrightarrow{\textrm{AL}}+u\overrightarrow{\textrm{LC}} \\
= & \left( \vec{q}+\vec{r} \right) +u \left( 2\vec{p}-\vec{r} \right) \\
= & 2u\vec{p}+ \vec{q}+(1-u)\vec{r} \quad \cdots [2]
\end{align*}
\(\vec{p} ,~\vec{q},~\vec{r}~\)は互いに一次独立であるから,\([1],~[2]\)より
\begin{align*}
\begin{cases}
s+2t= 2u \\
2s+t= 1 \\
s+t= 1-u
\end{cases}
\end{align*}
これを解いて\( s=\frac25,~t=\frac15,~u=\frac25. \)したがって
\[
\overrightarrow{\textrm{AP}}=\frac25 \overrightarrow{\textrm{AK}}+\frac15 \overrightarrow{\textrm{AI}} \quad \cdots \text{(答)}
\]
また,3点\(~\textrm{A,P,Q}~\)は一直線上に並んでいるので,
\begin{align*}
\overrightarrow{\textrm{AQ}}= & k\overrightarrow{\textrm{AP}} \\
= & \frac{2k}{5}\overrightarrow{\textrm{AK}}+\frac{k}{5}\overrightarrow{\textrm{AI}}
\end{align*}
を満たす実数\(~k~\)が存在する。
点\(\textrm{Q}~\)は,線分\(\textrm{KI}~\)上にあるから
\begin{align*}
\frac{2k}{5}+\frac{k}{5}= & 1 \\
k= & \frac{5}{3}
\end{align*}
したがって
\begin{align*}
\overrightarrow{\textrm{AQ}}= & \frac25 \cdot \frac53 \overrightarrow{\textrm{AK}}+\frac15 \cdot \frac53 \overrightarrow{\textrm{AI}} \\
= & \frac23 \overrightarrow{\textrm{AK}} +\frac13 \overrightarrow{\textrm{AI}}
\end{align*}
よって点\(~\textrm{Q}~\)は,線分\(~\textrm{KI}~\)を\(1:2\)に内分する点である。\(\therefore 2. \quad \cdots \text{(答)} \)
さらに詳しい解説授業もあります
この問題でさらに力をつけよう!詳しい解説授業はこちら
※誤植やミスを見つけた方は,ぜひお知らせください。






