[mathjax]
この記事には,久留米大学医学部の過去問の詳しい解説が載っています。過去問を通して久留米大学医学部の数学について学べるように,授業のような解説にしています。これまで勉強してきたことを整理し、あなたの数学力をレベルアップしましょう!
解答はすでにこちらの記事で示しております。
平成30年度(2018)久留米大学医学部一般入試数学[1]
典型的ではあるが,細かいところで差がつく問題
放物線,円,法線,とおなじみの直線や曲線に関する数Ⅱの問題です。手法は特に難しいものではありませんが,差が付くポイントがありますので,注意してみてみましょう。
「点Pの座標」はすぐわかる
問題文にはいろいろ書いてありますけれども、そのうち一部の情報から,点Pの座標はすぐに求められることが分かります。 まず解答を振り返ってみましょう。
点Pと円の中心を通る直線は,点Pにおける接線と垂直に交わる直線(法線)である。点Pにおける接線の傾きは\(~6~\)であるから,\(~y’=2x~\)より,点Pの\(~x~\)座標は\(~3.\)
したがって点Pの座標は\((x,~y~)=(3,~9). \quad \cdots \text{(答)}\)
問題文には「点Pと円の中心を通る直線の傾きは\(-\frac16\)」とありますが,点Pは放物線と円が接している点です。ですから「点Pと円の中心を通る直線」とは放物線の点Pにおける法線であり,点Pにおける接線の傾きが6であることがわかります。
放物線上の点で,その点における接線の傾きが6になる点は1つしかありません。ということで,点Pはただ一つに定まることがすぐにわかるのです。
ここまでの思考は,1分ほどで終わらせたいところです。
\(a,~b~\)の関係式を2つつくって連立する
\(b~\)の値を求めるために,\(b~\)についての関係式をつくります。もう一つ不明な文字定数\(a~\)がありますので,\(a,~b~\)の関係式をつくり,連立して求めることになります。
点Pの座標がわかったので,点Pにおける法線を作ることは簡単です。それが円の中心\( (a,~b )\)を通ることから,関係式を1つつくることができます。また,点Pが円上の点であることからも,関係式を1つつくることができます。
点Pにおける法線の方程式は
\begin{align*} y=&-\frac16(x-3)+9 \\ =&-\frac16x+\frac{19}{2} \end{align*} これが円の中心\((a,~b)\)を通るので \begin{align} b=&-\frac16a+\frac{19}{2} \\ 6b=& -a+57 \\ a=& 57-6b \label{eq:ks301-1} \end{align}(点Pと円の中心との位置関係より,\(a>3,~0~\verb|<|~b~\verb|<|~9.\) )
また,点P\((3,~9)\)は円\( ~(x-a)^2+(y-b)^2=b^2~\)上にあるので
\begin{align} (3-a)^2+(9-b)^2=b^2 \label{eq:ks301-2} \end{align}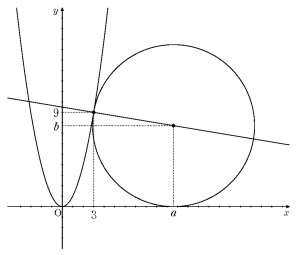
結局,次の2つの関係式が出来ました。 \begin{align*} a&=57-6b \\ (3-a)^2&+(9-b)^2=b^2 \end{align*} あとは連立するだけですが・・・括弧の部分を見てください。ここをこの時点で考えたかどうかで,この後の流れが変わってきます。括弧に気付いていない人は,問題を解くのにちょっと時間がかかるかもしれません。
\(a,~b~\)の範囲を事前に絞っておけば,計算が楽になる。
ここまではみんな似たようなものでしょう。ここから,左辺を展開する人と展開しない人に分かれます。展開した場合どうなるかを見てみましょう。
\begin{align*} 37(9-b)^2&=b^2 \\ 36b^2-18\cdot 37b+9\cdot 37&=0 \\ 4b^2-2\cdot 37b+9\cdot 37&=0 \\ 4b^2-74b+306&=0 \\ \end{align*}
\(306=9\cdot37\)であることに注意して\begin{align*} b&=\frac{37 \pm \sqrt{37^2-4\cdot306}}{4}\\ &=\frac{37\pm\sqrt{37(37-4\cdot9)}}{4}\\ &=\frac{37\pm\sqrt{37}}{4} \end{align*}
点Pと円の中心の位置関係より\(~b<9~\)なので, \begin{align*} b=\frac{37-\sqrt{37}}{4} \cdots \text{(答)} \end{align*}2次方程式を解くだけなので,答えは出ますけれども,うまく工夫しないと数字が大きくなってめんどくさくなります。また,最後のところでマイナスの方だけになることに気付かず,プラスマイナス両方を答えとした人もいるのではないでしょうか。
こちらで解いた人は,ミスをしないよう細心の注意を払って解いていくことが必要です
では,前述の括弧に気付いていた人はどう解くのでしょうか。それは,2次方程式を展開せず,1次方程式にして解くのです。
\(b\)の範囲が,点の位置関係から\(~0 < b < 9~ \)であることに気付いているので,両辺ともルートをとって1次方程式にすることができます。そうすれば,解は1つに定まるので,特にミスをするようなところもありません。こちらの方が,正解にスムーズにたどり着けることがわかるでしょう
ちょっとしたことではありますが,数の範囲を絞ることができるときはなるべく絞っておきましょう。
この問題のポイント
振り返ってみましょう。
この問題が解けるかどうかのポイントは、
- 点Pの座標を瞬殺で求めることができる。
- 問題文から2つの式を立て,連立することができる
- \(a,~b~\)の範囲を絞り込んでおくことで,ミスが少ない解き方ができるか
です。正解したとしても,なるべくミスが少ない解法を選べるようになっておきましょう。






